Chromaticity is an objective specification of the quality of a color regardless of its luminance. Chromaticity consists of two independent parameters, often specified as hue (h) and colorfulness (s), where the latter is alternatively called saturation, chroma, intensity, or excitation purity. This number of parameters follows from trichromacy of vision of most humans, which is assumed by most models in color science.
Quantitative description
In color science, the white point of an illuminant or of a display is a neutral reference characterized by a chromaticity; all other chromaticities may be defined in relation to this reference using polar coordinates. The hue is the angular component, and the purity is the radial component, normalized[clarification needed] by the maximum radius for that hue.
Purity is roughly equivalent to the term “saturation” in the HSV color model. The property “hue” is as used in general color theory and in specific color models such as HSL and HSV color spaces, though it is more perceptually uniform in color models such as Munsell, CIELAB or CIECAM02.
The CIE 1931 xy chromaticity space, also showing the chromaticities of black-body light sources of various temperatures, and lines of constant correlated color temperature
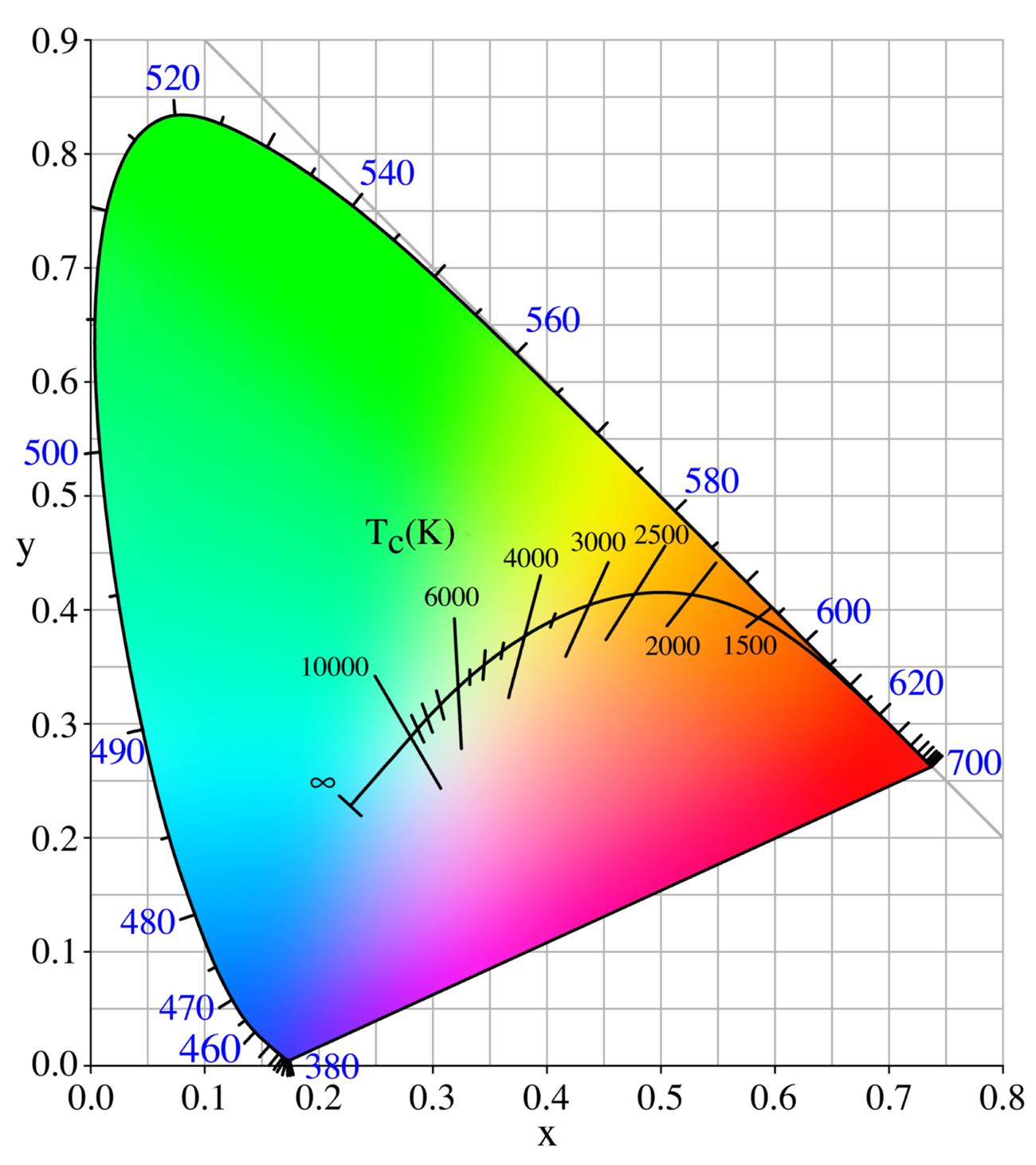
Some color spaces separate the three dimensions of color into one luminance dimension and a pair of chromaticity dimensions. For example, the white point of an sRGB display is an x, y chromaticity of (0.3127, 0.3290), where x and y coordinates are used in the xyY space.
(u′, v′), the chromaticity in CIELUV, is a fairly perceptually uniform presentation of the chromaticity as (another than in CIE 1931) planar Euclidean shape. This presentation is a projective transformation of the CIE 1931 chromaticity diagram above.

(u′, v′), the chromaticity in CIELUV, is a fairly perceptually uniform presentation of the chromaticity as (another than in CIE 1931) planar Euclidean shape. This presentation is a projective transformation of the CIE 1931 chromaticity diagram above.
These pairs determine a chromaticity as affine coordinates on a triangle in a 2D-space, which contains all possible chromaticities. These x and y are used because of simplicity of expression in CIE 1931 (see below) and have no inherent advantage. Other coordinate systems on the same X-Y-Z triangle, or other color triangles, can be used.
On the other hand, some color spaces such as RGB and XYZ do not separate out chromaticity, but chromaticity is defined by a mapping that normalizes out intensity, and its coordinates, such as r and g or x and y, can be calculated through the division operation, such as x = X / X + Y + Z, and so on.
The xyY space is a cross between the CIE XYZ and its normalized chromaticity coordinates xyz, such that the luminance Y is preserved and augmented with just the required two chromaticity dimensions.